量子色力学

量子色力学（りょうしいろりきがく、英語: quantum chromodynamics、略称: QCD）とは、素粒子物理学において、SU(3)ゲージ対称性に基づき、強い相互作用を記述する場の量子論である。

標準模型
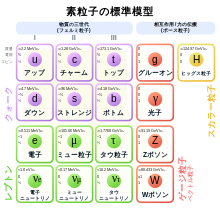
標準模型の素粒子
背景 素粒子物理学 場の量子論 ゲージ理論 自発的対称性の破れ ヒッグス機構 構成要素 電弱相互作用 量子色力学 CKM行列 制約 強いCP問題 階層性問題 ニュートリノ振動 理論家 スダルシャン · マーシャク · ファインマン · ゲルマン · 坂田 · グラショー · ツワイク · 南部 · ハン · カビボ · ワインバーグ · サラーム · 小林 · 益川 · トホーフト · フェルトマン · グロス · ポリツァー · ウィルチェック

色

陽子と中性子の量子色力学

クォークとグルーオンは、カラーチャージと呼ばれる量子数を持つ。カラーチャージは、光の三原色からの類推により「赤」、「緑」、「青」と呼ばれることがある。 カラーチャージを持たない状態は「白色」であるとも呼ばれる。これは SU(3) リー代数の表現を分かりやすい言葉で表したものである。クォークは SU(3) の基本表現 3（三重項）を作り、反クォークは基本表現 3（反三重項）をなす。3 は「色」の類推で言えば「補色」に対応している。グルーオンは随伴表現 8（八重項）で、「色」と「補色」を共に持つ8つの状態がある（3 × 3 から、「白色」（一重項）となる組み合わせが取り除かれる）。

カラーチャージはグルーオンと呼ぶゲージ粒子を交換することでやり取りされ、これが強い相互作用の源になっている。この相互作用はカラーチャージ間の距離が小さくなる（交換される運動量が高くなる）と弱くなるという、漸近的自由性を示す。逆に距離が大きくなると相互作用が強まり一定の力に近づく。この結果クォークを単体で取り出すことはできない。これは、現実に観測されるハドロンの状態は「白色」に限られるという、クォークの閉じ込め現象を説明する。

「白色」状態を作るには、三原色を持つクォークと「補色」となるカラーチャージをもつ反粒子とでペアを作る（メソン）か、3つのクォークについて3つの三原色を重ねて「白色」となるようにトリオを作る（バリオン）かが考えられる。SU(3) の表現論の言葉で言えば、

3 × 3 = 1 + 8

3 × 3 × 3 = 1 + 8 + 8 + 10

に現れる 1 がそれぞれメソンとバリオンに対応している。グルーオンのみからも「白色」の状態を作ることができる。そのような粒子はグルーボールと呼ばれる。最も簡単なグルーボールをSU(3) の表現論の言葉で言えば、

8 × 8 = 1 + 8 + 8 + 10 + 10 + 27

に現れる1が対応している。また、これらの他に「白色」となる状態の可能性もあり、それらはエキゾチックであると呼ばれる。2003年に報道されたペンタクォークやテトラクォークはエキゾチックな粒子（エキゾチックハドロン）の例である。 テトラクォークをSU(3) の表現論の言葉で言えば、

3 × 3 × 3 × 3 = 1 + 8 + 8 + 10 + 8 + 10 + 1 + 8 + 27

に現れる1が対応している。

カラーチャージを持つことは、強い相互作用をするということと同じことである。それゆえ、電子やニュートリノなどのレプトンや電磁相互作用のゲージ粒子である光子はカラーチャージを持っていない。

歴史

強い相互作用の現代的イメージの起源はクォーク模型である。1964年、ゲルマンとツワイクによりクォークが導入された。その後、クォークの束縛状態であるハドロンのパウリ統計の問題から“新しい”自由度、カラーがハン、南部、グリーンバーグにより提唱された。一方で、QCDの理論的基礎は1954年に発表されていた、ヤンとミルズによる非可換ゲージ理論である。しかし、この理論は質量ゼロのベクトル粒子（つまり、長距離相互作用する粒子）をふくみ、1fm以下のスケールの現象の記述を目指す理論としては不満足なものだった。さらにこの当時は非可換ゲージ理論の繰り込み可能性は証明されていなかった。そして、南部はカイラル対称性やその自発的破れなどを提唱し、1970年代に入ると、非可換ゲージ理論の繰り込み可能性や漸近的自由性がようやく証明され、QCDは脚光を浴びるようになる。

漸近的自由性により、高エネルギーでは相互作用が弱くなり摂動論による計算が可能となるのに対し、低エネルギーでは相互作用が強くなり摂動論が破綻するため、この理論の基本粒子であるクォークやグルーオンが単体で観測できない問題（クォークの閉じ込め）に関する解析は困難であったが、1974年にケネス・ウィルソンにより提案された格子ゲージ理論を用いた定式化により、強結合領域における計算が原理的に可能となった。その後、コンピュータの発展によりモンテカルロ法による数値シミュレーションが可能となり、クォークの閉じ込めの説明や様々なハドロンの質量の計算がなされている。

定式化

量子色力学（以下、QCDと表記）はゲージ群 SU(3) に基づくヤン＝ミルズ理論である。カラー SU(3) の電荷を持つディラック場（クォーク）同士の相互作用を媒介するゲージ場はグルーオンである。

グルーオンと相互作用するディラック場についてのQCDラグランジアン密度は以下のように記述される。

${\mathcal {L}}_{\text{QCD}}=\sum _{\psi }\left(i{\bar {\psi }}^{j}\gamma ^{\mu }({\mathcal {D}}_{\mu }\psi )_{j}-m_{\psi }{\bar {\psi }}^{j}\psi _{j}\right)-{\frac {1}{4}}G_{\mu \nu }^{a}G^{a\mu \nu }$

ここで、ディラック場 $\psi _{j}$ はカラーの添え字 $i=1,2,3$ を持ち、その共変微分は

$({\mathcal {D}}_{\mu }\psi )_{j}=\partial _{\mu }\psi _{j}-ig_{s}G_{\mu }^{a}[T^{a}]_{j}{}^{k}\psi _{k}$

である。 g_s は強い相互作用のゲージ結合定数で、T^a（a=1,...,8） は SU(3) の生成子である。

$G_{\mu }^{a}$ はSU(3)_c のゲージ場、即ちグルーオンである。 ゲージ場の強度は

$G_{\mu \nu }^{a}=\partial _{\mu }G_{\nu }^{a}-\partial _{\nu }G_{\mu }^{a}+g_{s}f^{abc}G_{\mu }^{b}G_{\nu }^{c}$

となる。 ここで f^abc は SU(3) の構造定数である。

ラグランジアンに

${\mathcal {L}}'_{\text{QCD}}={\mathcal {L}}_{\text{QCD}}+{\frac {g_{s}^{2}\theta }{16\pi ^{2}}}G_{\mu \nu }^{a}{\tilde {G}}^{a\mu \nu }$

という変換を施しても運動方程式は変化しない。 ここで ${\tilde {G}}^{a\mu \nu }=\epsilon ^{\mu \nu \rho \sigma }G_{\rho \sigma }^{a}$ である。

関連項目

• ハドロン - クォークによって構成される粒子
  • メソン - クォークと反クォークのペアからなるハドロン
  • バリオン - クォーク3個からなるハドロン
  • ペンタクォーク - クォーク、反クォーク合わせて5個からなるハドロン
  • テトラクォーク - クォーク、反クォーク合わせて4個からなるハドロン
• アクシオン
• 繰り込み群
• ヤン＝ミルズ理論
• ヤン-ミルズ方程式と質量ギャップ問題
• 格子ゲージ理論