ヘインズ=ウルフプロット
生化学において、ヘインズ=ウルフプロット(英: Hanes–Woolf plot)は、初めの基質濃度 [S] と反応速度 v の比を [S] に対してプロットした酵素反応速度論のグラフ表現である。以下に示すミカエリス・メンテン式の変形に基づいている。
上式において、Kmはミカエリス・メンテン定数、Vmaxは最大反応速度である。
J・B・S・ホールデンは、この手法はバーネット・ウルフ(Barnet Woolf)によるものであると記した[1]。また、チャールズ・サミュエル・ヘインズ(Charles Samuel Hanes)もこの手法を用いたが、ヘインズはウルフについては言及も引用もしていない[2]。ヘインズはこの種の線型変換から反応速度論的パラメータを決定するために線型回帰を用いると、vではなく1/vの観測値および計算値との間で最も適合するような結果を生成するため、この手法には欠陥があると指摘した。
式はミカエリス・メンテン式から以下のように導くことができる。
逆数を取り [S] をかけると、
変形すると、
となる。
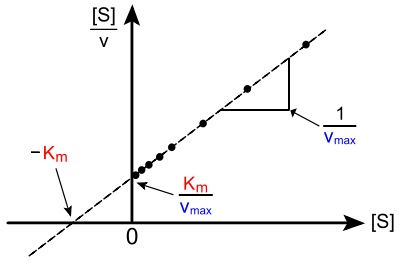
上式から明らかなように、完璧なデータからは傾き1/Vmax、y切片Km/Vmax、x切片−Kmの直線が得られる。
ミカエリス・メンテン式を線型化するその他の手法と同様に、ヘインズ=ウルフプロットはKm、Vmax、Vmax/Kmといった重要な反応速度論的パラメータを迅速に決定するために歴史的に使用されていたが、はるかに正確である非線型回帰手法に取って代わられている。しかしながら、データをグラフを使って示す方法としては引き続き有用である。
ヘインズ=ウルフプロットの1つの欠点は、縦座標と横座標のどちらも独立変数を表わさない点である(どちらも基質濃度に依存している)。その結果、適合度の典型的な指標である相関係数Rを適用できない。
脚注 編集
- ^ Haldane, J. B. S. (20 April 1957). “Graphical Methods in Enzyme Chemistry”. Nature 179 (832). doi:10.1038/179832b0.
- ^ Hanes, CS (1932). “Studies on plant amylases: The effect of starch concentration upon the velocity of hydrolysis by the amylase of germinated barley.”. Biochemical Journal 26 (5): 1406–1421. PMC 1261052. PMID 16744959.
![{\displaystyle {[S] \over v}={[S] \over V_{\max }}+{K_{m} \over V_{\max }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cfabea4f5fe6b4c2e6533f824b5f15aefc18218)
![{\displaystyle v={{V_{\max[}S]} \over {K_{m}+[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe8e1abf595d0f2b2941797aa98e1784cb21452)
![{\displaystyle {[S] \over v}={{[S](K_{m}+[S])} \over {V_{\max[}S]}}={{K_{m}+[S]} \over {V_{\max }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/205ac16a4c5734f25049d68170b38505062b7342)
![{\displaystyle {[S] \over v}={1 \over V_{\max }}[S]+{K_{m} \over V_{\max }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bb781047fcb26179df1b93d6d8c0cde115a59b4)