ベルヌーイ試行
確率論や統計学において、ベルヌーイ試行(ベルヌーイしこう、英語: Bernoulli trial)または二項試行(にこうしこう、英語: binomial trial)とは、取り得る結果が「成功」「失敗」の2つのみであり、各試行において成功の確率が同じであるランダム試行である[1]。この名前は、17世紀のスイスの数学者であるヤコブ・ベルヌーイにちなんで名付けられた。ベルヌーイは、1713年の著書『推測法』(Ars Conjectandi)でこの試行を分析した[2]。
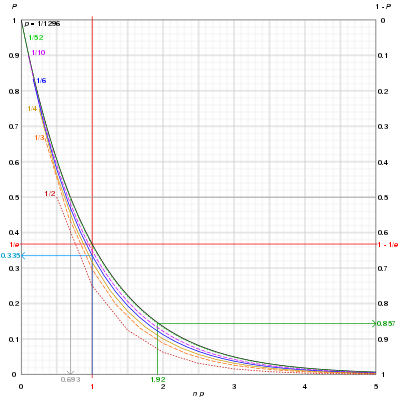
青い線: 6面のサイコロを6回投げて、6(または任意の数字)が1度も出ない確率は33.5%である。n 回の試行で確率 1/n の事象が発生しない確率が、n が増加するにつれて0に近づいて行く様子が確認できる。
灰色の線: ヤッツィー(5個のサイコロを投げて全て同じ目になること)になる確率を50%にするためには、0.693 × 1296 ~ 898 回試行する必要がある。
緑色の線: ジョーカーを除いたトランプの山からカードを1枚引いて山に戻す試行を100回(= 1.92 × 52)繰り返したとき、エースを少なくとも1回引く確率は85.7%である。
ベルヌーイ試行の数学的形式化をベルヌーイ過程という。本項目ではベルヌーイ試行の基本的な概念を説明する。より高度な処理についてはベルヌーイ過程を参照のこと。
ベルヌーイ試行の結果は2つしかないため、以下のような「はい」か「いいえ」かで答えられる質問として組み立てることができる。
すなわち、結果の「成功」「失敗」とは単なるラベルであり、文字通りの意味として解釈されるべきではない。この場合の「成功」という用語は、道徳的な判断ではなく、結果が指定された条件に合致するかどうかを意味する。
より一般的には、特定の事象(結果の集合)についての任意の確率空間が与えられたとき、その事象が発生したかどうか(事象または余事象)に対応するベルヌーイ試行を定義できる。ベルヌーイ定義の例として、以下のものが挙げられる。
定義
編集取り得る結果が正確に2つである試行を繰り返し実施し、各試行が独立している場合、この試行をベルヌーイ試行という。結果のうちの1つを「成功」、それ以外の結果を「失敗」と呼ぶ。ここで、1回のベルヌーイ試行で成功する確率を 、失敗する確率を とする。このとき、失敗は成功の余事象であるため、成功の確率と失敗の確率を合計すると1になる。「成功」と「失敗」は相互排他的かつ網羅的(MECE)である。従って、次式の関係がある。
これらはオッズの観点で記述することもできる。成功の確率 p と失敗の確率 q を与えたとき、成功のオッズ (odds for)は 、失敗のオッズ (odds against)は である。次式のようにこれを割り算と解釈すると、数値として表現できる。
これらは互いに逆数であり、掛けると1になる。
あるベルヌーイ試行が、有限回の同様に確からしい結果における事象を表しており、成功が S 回、失敗が F 回であった場合、成功のオッズは 、失敗のオッズは である。これにより、確率とオッズについて次の式が得られる。
ここで、確率ではなく結果の数を除算することでオッズを計算しているが、これらの比率は両方の項に同じ定数係数を乗算することのみが違うため、比率は同じである。
ベルヌーイ試行を記述する確率変数は、多くの場合、1 =「成功」、0 =「失敗」という規則を使用してエンコードされる。
二項試行は、ベルヌーイ試行に密接に関連している。独立したベルヌーイ試行の回数を 、それぞれの成功の確率を とし、成功数をカウントする。二項試行に対応する確率変数は で示され、二項分布を持つ。試行 において成功が 回であったときの確率は次式で与えられる。
ここで、 は二項係数である。
また、ベルヌーイ試行は、負の二項分布 (一連の繰り返されるベルヌーイ試行において、指定された数だけ失敗するまでの成功数の分布)などの様々な確率分布につながる。
複数のベルヌーイ試行が実行され、それぞれに別の成功の確率がある場合、これをポアソン試行という[3](ポアソン二項分布も参照)。
例:コイントスの場合
編集公正なコインを4回投げて、表が出る回数が2回となる確率を考える。
解
編集この試行では、表が出ること「成功」、裏が出ることを「失敗」と定義する。コインは公正であると想定されているため、成功の確率 p は である。従って、失敗の確率 は次式で与えられる。
上記の式を使用して、4回のコイントスのうち表が出る回数が2回となる確率は、次式のように求められる。
関連項目
編集脚注
編集- ^ Papoulis, A. (1984). "Bernoulli Trials". Probability, Random Variables, and Stochastic Processes (2nd ed.). New York: McGraw-Hill. pp. 57–63.
- ^ James Victor Uspensky: Introduction to Mathematical Probability, McGraw-Hill, New York 1937, page 45
- ^ Rajeev Motwani and P. Raghavan. Randomized Algorithms. Cambridge University Press, New York (NY), 1995, p.67-68
外部リンク
編集- Hazewinkel, Michiel, ed. (2001), “Bernoulli trials”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- “Simulation of n Bernoulli trials”. math.uah.edu. 2014年1月21日閲覧。