偏差値
偏差値(へんさち、英: T-score)とは、データの値を、平均50、標準偏差10のデータに変換(標準化)した値である。個々のデータに対して平均からどれだけ離れているか感覚的に現す方法である。データの単位を消して一律の指標として表すことを目的とするので、結果的に無次元数となる。
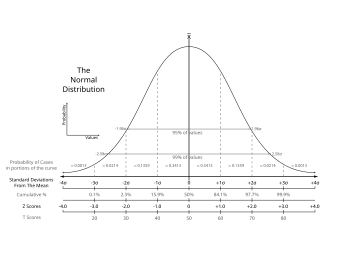
計算方式から、偏差値50のデータは平均である。偏差値50±5以内とは以内を意味するので、全体のうち平均に近い68.26%分のデータに含まれることを意味する。同様にして右の図のような分布に従うと考えて、平均からの離れ具合を求める。
学力試験・テストに導入されている学力偏差値は、受験者の得点が受験者全体の中でどの程度高い(低い)位置を知ることができる指標である。一般的なテストでは通常、偏差値は25(下位0.62%)前後から75(上位0.62%)の範囲に収まることが多いとされる[1]。しかし、極端な分布では、偏差値が100を超えたりマイナスになることもありえる。
概要 編集
偏差値とは、データを平均50、標準偏差(スケール)を10に標準化したときの値のことである。異なるデータでの偏差値の比較は、データが正規分布に近いことを前提としている。したがって、データが正規分布に大きく従わない場合は、偏差値は必ずしも適切な指標とはいえない(平均が最頻値であることが望ましい)。
正規分布であるデータにおいて、平均50からの±10区間(40~60)は全体の約68.3%、±20区間(30~70)は約95.4%、±30区間(20~80)は約99.73%、±40区間(10~90)は約99.9937%、±50区間(0~100)は約99.999953%である[2]。
- 偏差値60以上(あるいは40以下)は、上位(下位)15.866%。
- 偏差値70以上(あるいは30以下)は、上位(下位)2.275%。
- 偏差値80以上(あるいは20以下)は、上位(下位)0.13499%。
- 偏差値90以上(あるいは10以下)は、上位(下位)0.00315%。
- 偏差値100以上(あるいは0以下)は、上位(下位)0.00002%。
例えば、全受験者数が100万人の学力試験の場合、偏差値80以上の者は、ほぼ1350人となる(日本の実際の統計では、10代における同じ年齢の人口はおおよそ110〜120万人程度。40代は180〜200万人程度)。
偏差値は全ての実数を取りうるが、偏差値が±50区間(0~100)を外れる割合は非常に低く、約0.000047%、つまり約200万分の1しかない。
偏差値による優劣の判断は元の数字の特性に依存する。学力テストなど高い得点ほど良い場合は偏差値が高いほど良いとされる。また、ゴルフのスコアのように低い得点ほど良い場合は、偏差値も低い方が良いとされる。射的など目標にどれだけ近いかとする場合は中心である50が最も良いとされ、それから離れるほど悪い結果とされる[3]。
数式による表記 編集
データの値 xi に対する偏差値 Ti は次の式で定義される[4]。
ここで、
なお、分子 xi − μx は偏差である。特に、値 xi が平均値 μx に等しいときは、偏差が 0 となり、偏差値は 50 となる。また、値 xi が全て等しいときは、標準偏差 σx = 0 となり、偏差値がこの式では定義できない。この場合、値の偏差値を全て 50 とする[5]。
用例 編集
正しい用例 編集
- 学力検査の結果を表す学力偏差値は、入学試験の合格率の判定などに広く使われている。
- 製造業の品質管理の結果として偏差値が使われる。この場合で仕様に上限および下限がある場合50が最も良い状態とされ、上限下限より数値が離れているものはより不良品と判断される。
- 知能検査の結果を表す知能偏差値は、教育などに役立てるために、知能指数などとともに使われている。
比喩、例え、俗語、スラングによる使用例 編集
- 何らかの「格付け」として、数値化せず比喩的に「○○偏差値」という言葉や概念が用いられることがある(恋愛偏差値、顔面偏差値、就職偏差値など)。この場合は一般に高い方が良いとする。
脚注 編集
- ^ “偏差値とは何?偏差値の意味と求め方・計算方法をわかりやすく解説!|栄光の個別ビザビ|個別指導の塾・学習塾なら”. www.eikoh-vis-a-vis.com. 2022年7月1日閲覧。
- ^ 大國 亨 オプション理論
- ^ “偏差値って何ですか?|よくある質問|マナビジョンラボ”. manabi.benesse.ne.jp. 2023年2月27日閲覧。
- ^ “6-3. 偏差値を求めてみよう | 統計学の時間 | 統計WEB”. 2023年2月27日閲覧。
- ^ “偏差値の求め方。正しい計算方法は?自分でもできる?専門家に聞きました! / 【スタディサプリ進路】高校生に関するニュースを配信”. 高校生なう. 2023年2月27日閲覧。
