行列式
数学における行列式(ぎょうれつしき、英: determinant)とは、正方行列に対して定義される量で、歴史的には行列が表す一次方程式の可解性を判定する指標として導入された。幾何的には線型空間またはより一般の有限生成自由加群上の自己準同型に対して定義され、線型変換に対して線形空間の拡大率ということができる。行列の可逆性を判定する指標として線型代数学における最も重要な指標の一つと見なされている。
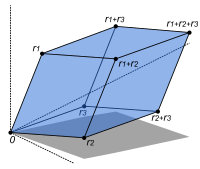
概要 編集
X を実2次正方行列
とするとき、これは
という平面上の線型変換を定めている。一方で、2つの平面ベクトル u = (u0, u1), v = (v0, v1) に対して、これらが張る平行四辺形の「向きも込めた」面積は
により指定されると考えることができる。このとき A(Xu, Xv) = (ad − bc)A(u, v) が成り立っているが、これは X の定める線型変換によって平面内の図形の面積が (ad − bc) 倍される、と解釈できる。
したがって、実2次正方行列 X に対して(上の記号の下で)det X ≔ ad − bc を対応させると、det(XY) = (det X)(det Y) であることや、det X > 0 であるとき X の定める変換は図形の向きを保ち、反対に det X < 0 であるとき図形の向きは反転させられることが分かる。det の乗法性から X が可逆ならば det X は逆数を持つ数であることが従うが、反対に X が退化した行列(つまり X の定める変換の像が一次元の部分空間)になる場合にはすべての図形の変換後の面積が 0 になることから det X = 0 となることがいえる。こうして、正方行列 X が正則であることと X の行列式が可逆であることは同値であることが分かる。
同様にして一般の次数のN次正方行列 X に対し、X の定める線型変換が超立体(N次図形)の超体積を何倍にしているかという符号付き拡大率を X の行列式として定義することができる。これは行列の成分を変数とする多項式の形で書け、二次の場合と同様にこれは正則性など正方行列の重要な性質に対する指標を与えている。一次方程式系が与えられるとき、方程式の係数行列に対してその行列式の値を調べることにより、方程式系の根の状態をある程度知ることができる。特にクラメルの公式により、根が一組である線型方程式系の根の公式が行列式を用いて表示される。
定義 編集
抽象的な定義 編集
K を可換環とし、E を階数 n の A 上の自由加群とする。E の n-次外冪 ⋀nE は A 上階数1の自由加群である。E 上の K-線型写像 ϕ について、⋀nE 上に引き起こされる K-準同型
は一意的に定まるある a ∈ A に関する定数倍写像と一致する。この a は ϕ の行列式 det ϕ と呼ばれる。
明示的な定義 編集
n 次正方行列 A の i 行 j 列成分を ai,j で表すと、A の行列式は、次の式で定義される:
ここで、
を表す。
n 次正方行列の行列式は n 次の斉次多項式で、項を n! 個持つ(ライプニッツの公式)。
正方行列 A の行列式は、|A| あるいは det(A) と表記される。行列の成分を明示する場合は
を単に
と書く。
二つの定義の同値性 編集
Kn の標準基底を (e1, …, en) とする。正方行列 X を表す列ベクトルを v1, …, vn とすると、vj = Xej である。
であるが、ここで
である。ただし、vi の第 i 成分を v j
i と表した)。これは Kn 上 ⋀nX が (det X)-倍写像として作用していることを示している。
n-次外積の普遍性により、行列式とは、行列の各列のベクトルに関する n-重交代線型写像で単位行列には 1 を与えるものとして特徴づけられることが分かる。
複線型交代形式 編集
n次行列に関する行列式は列に関して n重交代線型性をもつ[1]。つまり、行列を (a1, a2, …, an) のように列ベクトルの組の形に書くことにすれば
が成り立っている。例えば、線型性によって
が成立しており、さらに交代性によって
も成り立っている。特に、どれか二つの列が全く同一の成分を持つような行列の行列式は 0 である[2]。
A の行列式と、A の転置行列の行列式は等しい[3]。これによって、行列式が列に関してある性質を持てば、行に関しても同様の性質を持つことが分かる。つまり、上記の性質は全て行に対するものにも書き直せる。
二つの行列の積の行列式は、それぞれの行列式の積に等しい:A, B を n次正方行列とするとき、|A|⋅|B| = |AB| である。これより特に行列式が基底の取り替えによって不変であることが従う。
歴史 編集
西洋で行列式が考えられるようになったのは16世紀であり、これは19世紀に導入された行列そのものよりも遥かに昔に導入されていたことになる。また、数を表の形に並べたものや、現在ガウス(・ジョルダン)消去法と呼ばれているアルゴリズムは最も古くには中国の数学者たちによって考えられていたことにも注意する必要がある。
行列式に関する最初期の計算 編集
楊輝(中国、1238年? - 1298年)は『詳解九章算術』で数字係数の二元連立一次方程式の解をクラメルの公式の形で、行列式的なものを含んだ形で与えている。また1545年にジェロラモ・カルダノは、著書 Ars Magna の中で同じく2×2の場合のクラメルの公式を与えている。この公式は regula de modo(ラテン語で「様態に関するの規則」の意味)と呼ばれている。彼らは「行列式」を定義したわけではないが、その概念の萌芽を見てとることができる。
高階の行列に関する行列式 編集
高階の行列に関する行列式の定義はそれから百年ほどたって日本で和算の関孝和、田中由真、そしてドイツのライプニッツによりほとんど同時にかつ独立に与えられた。
関孝和ら和算家による発見 編集
関孝和は『解伏題之法』で行列式について述べている。本手稿のテーマは多変数の高次方程式から変数を消去して一変数の方程式に帰着することで、変数消去の一般的方法、つまり終結式の理論を提示している。本手稿では3次と4次に関しては行列式の正しい表示を与えているが、より高次の5次の場合はつねに0になってしまい、あきらかに間違っている。これが単純な誤記の類であるか否かは不明である。また、次節で述べるように、関西で活躍していた田中由真や井関知辰らの研究も同様の問題を考えており、類似の結果にたどり着いている。
これらの研究では、いずれも行列式は終結式を表すための手段にすぎず、行列式そのものを意味のある対象として捉えていたかについては異論がある。実際、それをあらわす用語すら提案されていない。また、日本が鎖国によって外界から遮断されていたこともあり、西洋数学に影響を与えることはなかった。
ライプニッツによる行列式の発見 編集
同じ時期にライプニッツは数多くの線型方程式系を研究していたが、その頃は行列記法がまだなかったので、彼は未知数の係数を、現在のような ai,j のかわりに ij のように添字の対によって表現していた。1678年に彼は3つの未知数に関する3つの方程式に興味を抱き、列に関する行列式の展開式を与えている。同じ年に彼は4次の行列式についても(符号の間違いを別にすれば)正しい式を与えている。ちなみにライプニッツはこの成果を公表しなかったので、50年後に彼とは独立に再発見されるまでこの成果は人々に認識されていなかった。
一般的な行列式 編集
関孝和は、最初の手稿からやや後の『大成算成』(建部賢明、建部賢弘と共著、執筆は1683年〈天和3年〉 - 1710年〈宝永7年〉頃)で、第一列についての余因子展開を一般の場合について正しく与えている。また、田中由真は『算学紛解』(1690年(元禄3年)ごろ)で 5次までの行列式を、井関知辰は『算法発揮』(1690年(元禄3年)刊)で第一行についての余因子展開を一般の場合で与えている。ちなみに関や田中の著作は写本のみであるが、井関の著作は出版がなされている。
ヨーロッパにおいても、行列式の理論は日本の場合と同じく(一次ではなく)高次の代数方程式の変数消去の研究のために発展した。1748年にマクローリンの(死後に刊行された)代数学の著作において4つの未知数に関する4つの方程式の系の解が正しい形で述べられ、行列式の研究が再開されることになった。1750年にクラメルは(証明抜きで)N 個の変数に関する N 個の方程式からなる方程式の解を求める規則を定式化した。この行列式の計算方法は順列の符号に基づく繊細なものだった。
ベズー(1764年)やファンデルモント(1771年、ヴァンデルモンドの行列式の計算)などがそれに続き、1772年にはラプラスによって余因子展開の公式が確立された。さらに翌年にはラグランジュによって行列式と体積との関係が発見されている。
今日の determinant(決定するもの)に当たる言葉が初めて現れたのはガウスによる1801年の Disquisitiones Arithmeticae である。そこで彼は二次形式の判別式(今日的な意味での行列式の特別な例と見なせる)を用いている。彼はさらに行列式と積の関係についても後少しのところまでいっている。
現代的な行列式の概念の確立 編集
現代的な意味での行列式という用語はコーシーによって初めて導入された[4]。彼はそれまでに得られていた知識を統合し、1812年には積と行列式の関係を発表している(同じ年にビネも独立に証明をあたえていた)。コーシーは平行して準同型の簡約化についての基礎付けの研究も行っている。
1841年に「クレレ誌」で発表されたヤコビの3本の著作によって行列式の概念の重要性が確立された。ヤコビによって初めて行列式の計算の系統的なアルゴリズムが与えられ、またヤコビアンの概念によって写像の行列式も同様に考察できるようになった。行列の枠組みはケイリーとシルベスターによって導入された。ちなみにケイリーは逆行列の公式を確立させており、行列式の記号として縦棒を導入したのも彼である[4]。
行列式の理論は様々な対称性を持つような行列についての行列式の研究や、線型微分方程式系のロンスキー行列式など数学の様々な分野に新たに行列式を持ち込むことが追究されている。
いくつかの行列式 編集
2次対称群 は恒等置換 id (id(1) = 1, id(2) = 2) と互換 σ = (1, 2)(σ(1) = 2, σ(2) = 1) の 2 つの置換からなるので
となる(第 1 項が id, 第 2 項が (1, 2) に対応する項である)。
2 次あるいは 3 次の正方行列については、左上から右下へ向かう方向に「+」、右上から左下へ向かう方向に「−」の符号を付けて積を取りそれらの和を取ると行列式が求められる。これを「サラスの方法」または「サラス展開」、「たすきがけの法」と言う。n 次正方行列に対して、サラスの方法で取り出せる項の数は高々 2n であり、一般には行列式の総項数 n! に比べてはるかに少ないため、4次以上の正方行列にはこの方法は使えない。
三角行列の行列式は、主対角成分の総乗をとることで求まる。三角行列の主対角成分には固有値が並ぶから、行列式の値は固有値の総乗である。このことは、基底の取替えによる行列の三角化可能性と行列式の乗法性によって、一般の正方行列に対しても正しい。つまり、与えられた行列の行列式の値は、その行列の固有値の総乗に等しい。
発展的な話題 編集
小行列式 編集
正方行列とは限らない一般の行列 A ≔ (aij) に対して、その行と列からそれぞれ k 個選び、それらに属する成分からなる正方行列の行列式を考えることができる:
これを A から作られる小行列式(しょうぎょうれつしき、minor determinant)という。行列に対して、0 でない小行列式の最大次数は行列の階数に一致する。特に、同じ番号の行と列を選んで
の形に書かれる(対角線上にある)小行列式を主小行列式(しゅしょうぎょうれつしき、principal minor)と呼ぶ。
余因子展開 編集
n次正方行列 A ≔ (aij) に対して、i 行または i 列を除いてできる小行列式に (−1)i+j を乗じた
を (i, j)余因子(よいんし、英: cofactor)という。(係数 (−1)i+j を含まない形で定義する場合もある。)
列(あるいは行)に関する線型性から、正方行列の行列式は、ある列(あるいはある行)の変数に関して斉 1 次である。A の行列式は j 列に関して
と展開される。また同様に i 行に関して
と展開される。(余因子の定め方によっては展開の符号が変わる。)
余因子は次数が 1 少ない行列式であるから、展開を繰り返すことで元の行列の行列式を小さなサイズの行列式の計算に帰着させることができる。基本変形に対する行列式の性質をうまく組み合わせると展開の効率を高めることができる。
余因子行列と逆行列 編集
n次正方行列 A ≔ (aij) に対し、(i, j)余因子を (j, i)成分に持つ行列
を A の余因子行列という。余因子行列については、余因子展開を逆に用いると
となることが確かめられる。ただし、En は n次単位行列である。またここから、A の行列式 det(A) が 0 でない場合には
なお、余因子行列としてここでの余因子行列の転置行列、すなわち (i, j)余因子を (i, j)成分に持つ行列 を採用する流儀もあるので、単に「余因子行列」といったときにはどちらの流儀であるか注意が必要である。
行列式の性質 編集
行列式の基本的な性質として以下が成り立つ。
- 転置の性質
- ある行列の転置行列の行列式の値はもとの行列式の値と変わらない。
- 行列式の行または列の入れ替えの性質
- 行列式の2つの行(または列)を入れ替えると、行列式の値は符号だけ変わる。
- 定数倍の性質
- 行列式の1つの行(または列)の各要素に一定の数cをかけた行列式の値は、もとの行列式の値のc倍になる。
- 同じ行があるときの性質
- 行列式の2つの行(または列)が行列式の一致する行列式なら、その行列式の値は0になる。
- 行列式の和の性質
- 行列式の1つの行(または列)の各要素が2つの数の和であるならば、その行(または列)を一方の数のみで置き換えた行列と、他方のみで置き換えた行列式との和になる。
- 行列式の計算則
- 行列式の1つの行(または列)の各要素に一定の数cをかけて他の行(または列)に加えても、行列式の値は変わらない。
- 行列の積の行列式
- n次の正方行列A,Bに関して|AB|=|A||B|が成り立つ。
固有値との関係 編集
行列 A の固有値を λi (i = 1, …, n) と置くと、
となる。このことは、A を三角化すると、対角成分に固有値が並ぶこと、すなわち
の両辺の det を取ることで得られる。
特異値との関係 編集
正方行列 A の特異値を σi(A) (i = 1, …, n) と置くと、
となる。このことは、特異値分解を用いて示される。
証明 — (対角行列Σの対角成分は非負)
正方行列 An に関して行列式と固有値および特異値の間には次の関係が成り立つ。
跡との関係 編集
正方行列の跡 (trace) とは、対角成分の総和である。それは固有値の総和に一致する。そのため、固有値の積である行列式とは指数関数 (exponential) を介してつながっている。 行列に対する指数関数は
と書けるが、A の固有値 λi とそれに属する固有ベクトル xi に対して、
となることより、exp(A) は固有値 exp(λi) とその固有ベクトル xi を持つことが分かる。よって、関係式
が成り立つ。
微分 編集
行列式は多項式であり、微分が可能である。余因子展開の式から、A の行列式 det(A) の微分として次の関係が成り立つ。
関連項目 編集
脚注 編集
参考文献 編集
- ニコラ・ブルバキ 著、銀林浩、清水達雄ほか 訳『代数』東京図書、東京、1968年。
- 行列と行列式の歴史に関する解説(英語)
- 「審査結果:「17世紀日本と18-19世紀西洋の行列式、終結式及び判別式」に対する審査結果(数学史の研究)」『数理解析研究所講究録』第1392巻、京都大学数理解析研究所、2004年9月、130-131頁、CRID 1050282677150617984、hdl:2433/49756、ISSN 1880-2818。
- Vein, R., & Dale, P. (2006). Determinants and their applications in mathematical physics (Vol. 134). Springer Science & Business Media.
- 西田吾郎『線形代数学』京都大学学術出版会、2009年6月22日。ISBN 978-4-87698-757-3。
- 数式処理のコンピューター(1)計算の完全機械化(未来技術)『日経産業新聞』1982年7月20日
- 和算の大家、関孝和没後300年庶民も愛した数学再興目指し記念の催し『東京朝刊』2007年11月11日
- 三宅敏恒『線形代数学-初歩からジョルダン標準形へ』培風館、2008年
- 中神祥臣、柳井晴夫:「矩形行列の行列式」、丸善出版、ISBN 978-4-621-06508-2(2012年12月)。※ 正方ではない行列に対して行列式を一般化する理論のひとつについての解説。
外部リンク 編集
- 『行列式の3つの定義・性質・意味』 - 高校数学の美しい物語
- 行列式の性質、KIT金沢工業大学、2013年7月14日
- 行列と行列式、大東文化大学、2014年12月12日
- 『行列式』 - コトバンク
- Weisstein, Eric W. "Determinant". mathworld.wolfram.com (英語).
- determinant in nLab
- determinant - PlanetMath.(英語)
- Definition:Determinant at ProofWiki
- Suprunenko, D.A. (2001), “Determinant”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4