イルミネーション問題

イルミネーション問題（Illumination problems）は、内側に反射率100パーセントの鏡を貼った閉曲線の中に点光源を1つ置いた時に、部屋の中の全てを照らすことができるか、という問題。

「ペンローズの照らせない部屋 (1958)」。青い線がペンローズが与えた閉曲線であり、この曲線内のどこに光源を置いても必ず影の部分ができる。

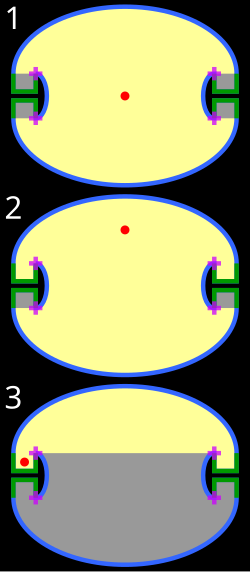
この問題をもう少し文学的に表現すると次のようになる。「壁一面が鏡張りの部屋でマッチに火をつけた時に、マッチが見えない場所が生じるような形の部屋はあるだろうか？」

原題は、アメリカの数学者エルンスト・ストラウスが1950年代に提起したと考えられている。

この問題は2つの仮説から成る。

仮説1. どのような閉曲線であっても、閉曲線内のどこに光源を置いても、閉曲線内の全ての場所に光が当たる。

仮説2. 仮説1が否定されたとしても、閉曲線内を完全に照らすことができる点が1つは存在する。

この問題に反例を与えたのは、ロジャー・ペンローズである。1958年にペンローズは楕円と直線で構成された「照らせない部屋（unilluminable room）」と呼ばれる閉曲線を発表した。この図形はストラウスの仮説を2つとも否定する。

「ペンローズの照らせない部屋」には曲線部分がある。1969年、ビクター・クレー（Victor Klee）はこの問題を「多角形」、つまり直線のみで作られた閉曲線なら成立するかどうかを提起した 。

1995年にTokarskyが示した直線26本の例、1997年にCastroが示した直線24本の例

この問題の仮説1に反例があることを示したのがジョージ・トカルスキー（George Tokarsky）である。トカルスキーは1995年に直線26本で作られたある閉曲線が反例となることを証明した。この図形の赤い点の位置に照明を置いた場合、一見全ての空間が照らされるように見えるが、×印の点だけには光が当たらない。さらにトカルスキーは、星形正二十角形2つを二等辺三角形に似た図形でつないだような形を例として「直角を使わない」という縛りを加えても解があることを示した。さらに3次元の例もあることを示している。さらには、光源を閉曲線上に置いてよいとするなら、凹四角形の最大内角を持つ点をC, その対頂点をB、残った頂点をA, Dとしたときに、AとDの内角が共に$x$、Bの内角が$2nx$の時には、点Aに光源を置いた場合には点Dには光が届かないことも示している。ただし、指定された点以外の位置に光源を置けば部屋は全て照らされるため、これらはストラウスの仮説2を否定するものではない。

1997年には直線24本での例（つまりより簡単な形の例）をトカルスキーとデイビッド・カストロ（David Castro）が独立に見つけた。

2016年、Lelièvre, Monteil, Weissは、多角形の各内角の大きさの比率が全て有理数で表せる場合、光が届かない点が生じる場合があることを示した。

外部リンク

• "The Illumination Problem - Numberphile", 教育用YouTubeチャンネルNumberphileでの解説（英語）。2017年2月28日。