フレシェ分布
フレシェ分布(英語: Fréchet distribution) は逆ワイブル分布としても知られている。フレシェ分布は、ガンベル分布(タイプIの極値分布)、ワイブル分布(タイプIIIの極値分布)とともに、一般化極値分布(英語: generalized extreme value distribution)の特別なケースである。フレシェ分布はタイプIIの極値分布と呼ばれる。
| 母数 |
形状母数. (以下の2つのパラメータを追加できる) 尺度母数 (標準分布で ) 位置母数 (標準分布で ) |
|---|---|
| 台 | |
| 確率密度関数 | |
| 累積分布関数 | |
| 期待値 | |
| 中央値 | |
| 最頻値 | |
| 分散 | |
| 歪度 | |
| 尖度 | |
| エントロピー | , ここで はオイラー・マスケローニ定数。 |
| モーメント母関数 | モーメント が ならば存在する。 |
フレシェ分布の名称は、フレシェ分布を発見した数学者モーリス・ルネ・フレシェに由来する[1]。
研究の発展
編集モーリス・ルネ・フレシェは、1927年に、Fréchet (1927) において、最大値の漸近分布を考察している[2][3]。フレシェ分布の研究は、さらに、ロナルド・フィッシャーとL・H・C・ティペットの1928年の共著論文によってなされている[4]。Fisher and Tippett (1928) は、極値分布がガンベル分布(タイプI)、フレシェ分布、ワイブル分布(タイプIII)の3つのいずれか1つのみであることを示した[4]。エミール・ユリウス・ガンベルは、フレシェ分布を含む極値分布の研究を詳細に行い、1958年に極値統計学の書籍をまとめた[5]。
定義と性質
編集フレシェ分布の累積分布関数は
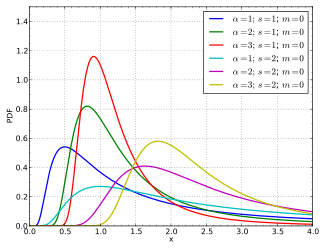
である (Alves & Neves 2011) 。ここで、α > 0は、形状パラメータである。フレシェ分布の確率密度関数は
となる。
フレシェ分布の期待値と分散は以下の通りとなる (Alves & Neves 2011)。
- 期待値は となる。
- 分散は となる。
ここで、 はガンマ関数であり、
である。
ガンベル分布(タイプI)、フレシェ分布(タイプII)、ワイブル分布(タイプIII)は、一般化極値分布として単一の分布関数で表現できる[6]。
一般化フレシェ分布
編集位置パラメータ m(最小値)と尺度パラメータs > 0を含めることで、フレシェ分布を一般化することができる[7]。 一般化フレシェ分布の累積分布関数は
である。 一般化フレシェ分布の確率密度関数は
となる。
応用例
編集- 水文学
- フレシェ分布は、1日当たり降水量の年間最大値のような極端な現象に適用される。
- 金融
- フレシェ分布は、市場収益をモデル化するために使われてきた[7]。
- 国際経済学(貿易論)
- リカード・モデルを連続財・多数国モデルに拡張した著名な研究 Eaton and Kortum (2002) は、国iの各財を生産する効率性 ( ) の分布が次のフレシェ分布に従うと仮定した[8]。
- ここで、 が形状パラメータ(定義式の )に相当する。 が小さいほど、効率性の分散が大きくなり、比較優位の役割が大きくなる。 は、分布の場所を左右する追加的なパラメータである。 が大きいほど、効率性が高められ、絶対優位が強くなる[8]。
脚注
編集注釈
編集出典
編集- ^ 高橋倫也 & 志村隆彰 2016.
- ^ Fréchet 1927.
- ^ Kotz & Nadarajah 2000.
- ^ a b Fisher & Tippett 1928.
- ^ Gumbel 1958.
- ^ Coles 2013, p. 47.
- ^ a b Alves & Neves 2011.
- ^ a b Eaton & Kortum 2002.
参考文献
編集- Alves, Isabel Fraga; Neves, Cláudia (2011). Lovric, Miodrag. ed (英語). Extreme Value Distributions. Berlin, Heidelberg: Springer. pp. 493–496. doi:10.1007/978-3-642-04898-2_246. ISBN 978-3-642-04898-2.
- Beirlant, Jan; Goegebeur, Yuri; Teugels, Jozef; Segers, Johan (2004-08-27) (英語). Statistics of Extremes: Theory and Applications. Wiley. doi:10.1002/0470012382. ISBN 978-0-471-97647-9.
- Coles, Stuart (27 November 2013) (英語). An introduction to statistical modeling of extreme values (eBook) (1 ed.). London: Springer London. doi:10.1007/978-1-4471-3675-0. ISBN 978-1-4471-3675-0. OCLC 883391507
- Eaton, Jonathan; Kortum, Samuel (2002-09). “Technology, Geography, and Trade” (英語). Econometrica 70 (5): 1741–1779. doi:10.1111/1468-0262.00352. ISSN 0012-9682.
- Eaton, Jonathan; Kortum, Samuel (2012-05). “Putting Ricardo to Work” (英語). Journal of Economic Perspectives 26 (2): 65–90. doi:10.1257/jep.26.2.65. ISSN 0895-3309.
- Fréchet, M (1927). “Sur la loi de probabilite de l'ecart maximum”. Ann. de la Soc. Polonaise de Math. 6: 93–116.
- Fisher, R. A.; Tippett, L. H. C. (1928-04). “Limiting forms of the frequency distribution of the largest or smallest member of a sample” (英語). Mathematical Proceedings of the Cambridge Philosophical Society 24 (2): 180–190. doi:10.1017/S0305004100015681. ISSN 1469-8064.
- Gumbel, E. J. (1958-03-02) (英語). Statistics of Extremes. Columbia University Press. doi:10.7312/gumb92958. ISBN 978-0-231-89131-8
- Kotz, Samuel; Nadarajah, Saralees (10 2000) (英語). Extreme Value Distributions. PUBLISHED BY IMPERIAL COLLEGE PRESS AND DISTRIBUTED BY WORLD SCIENTIFIC PUBLISHING CO.. doi:10.1142/p191. ISBN 978-1-86094-224-2.
- 高橋倫也、志村隆彰『極値統計学』(初版)近代科学社、2016年8月31日。ISBN 978-4-7649-7070-0。OCLC 961831235。
関連項目
編集- 確率分布
- 極値分布
- ガンベル分布(タイプIの極値分布)
- ワイブル分布(タイプIIIの極値分布)
- モーリス・ルネ・フレシェ










![{\displaystyle m+{\frac {s}{\sqrt[{\alpha }]{\ln 2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66ba8a89712c657b223f3b28708a6022e362f26c)



![{\displaystyle {\begin{cases}\ -6+{\frac {\Gamma \left(1-{\frac {4}{\alpha }}\right)-4\Gamma \left(1-{\frac {3}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+3\Gamma ^{2}\left(1-{\frac {2}{\alpha }}\right)}{\left[\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right]^{2}}}&{\text{for }}\alpha >4\\\ \infty &{\text{otherwise}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f0e101297df7d5cbc11a6a96d305a162371856d)



