エカント

エカント(Equantまたはpunctum aequans)は、天体の見かけの速さの変化を円運動で説明するために、古代ギリシャ天文学で用いられた、数学的な概念である。現存する文献では、2世紀にクラウディオス・プトレマイオスの『アルマゲスト』に最初に現れる。

プトレマイオスによる（水星を除く）惑星の運動。惑星（黄色）は周転円（小さい円）に沿って等速回転する。
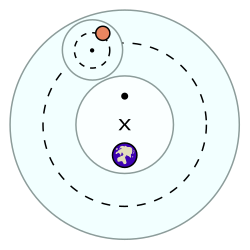
周転円の中心は、従円（大きい円）に沿って動く。ただし、従円の中心 X は地球の中心とは異なる。周転円の中心の運動は、エカント点（・）から見る角速度が一定となるように動く。

古代ギリシアでは、天体は円に沿って等しい速さで回転するとされた。しかし実際には、惑星の運動はケプラーの法則で示されるように、回転の半径も速度も一定ではない。このような運動を円を一つだけ用いて近似するために用いられたのが離心円とエカントである。

エカントは、簡単で精度のよい惑星の理論を実現させたが、同時にアリストテレス的な自然学の原則から外れ、物理的な根拠も明らかでなかったため、中世に置いてもしばしば批判される。エカントへの嫌悪がコペルニクスが地動説を考える大きな動機となり、彼の理論ではエカントは完全に排除された。一方、ケプラーは楕円軌道の理論に進む前に、エカントを用いた理論を作った。

離心円

ヒッパルコスは、太陽は地球と異なった点を中心とする円、すなわち離心円に沿って等速回転するとした。観測者が回転の中心から外れたところにいるため、見かけの太陽の速度は変化してみえる。これを太陽中心に書き直すと、地球を太陽から少し離れた点の周りに等速円運動させることで、ケプラーの法則を近似していることになる。軌道離心率が小さい場合、離心円の中心を(天体がない方の)楕円軌道の焦点とすると、二つの天体間の方向は精度よく近似できる。一方、距離の変動はあまりよく近似されない。

エカントと惑星理論

プトレマイオスは惑星の運動を説明するために、図のように二つの円を用いた。惑星(オレンジ色の点)は周天円とよばれる小さな円に沿って動く。一方、周天円の中心は点xを中心とする大きな円(従円または導円)に沿って動く。現代から見れば、これらの円の片方は地球の公転、もう一つは惑星の公転に対応している。従円は離心円となっていて、その中心xは地球からずれている。また周天円の中心はエカントと名付けられた点から見て一定の速度で動く。

このようにすると、周天円の方向だけでなく、地球からの距離の変動もよく近似できる。この距離の変動は周天円の大きさの変動として観測される。それゆえヒッパルコスの太陽の理論のように、回転の中心を点xにしてしまうと、観測にあわない理論になってしまう。

ケプラーのエカントの理論と楕円軌道の比較

ケプラーは楕円軌道の理論に進む前には、エカントで惑星の運動を説明していた。すなわち、地球を含む各々の惑星は、太陽の周りを離心円に沿って回る。回転の速さはエカントから見て一定になるように調節した。この理論は、太陽とエカントを楕円の焦点に一致させると、ケプラーの法則を非常によく近似する。この理論はコペルニクスの理論よりも単純で精度も高かった。

上記の惑星の理論で、地球から見た周転円の中心の方向の角度$\nu$を、もっとも地球に近接した地点から測ると、

$\nu (t)=\Omega t+2e\sin(\Omega t)+e^{2}\sin(2\Omega t)+O(e^{3})$

である。ここでtは時刻で、周転円の中心が地球に最も近いときに$t=0$とし、$\Omega$はエカントから見た一定の角速度、$e$は離心率、即ち従円の中心とエカントの距離を従円の半径$a$で割ったものである。（$\nu$は真近点角に, $\Omega t$は平均近点角に相当する。）また、地球から周転円の中心までの距離$r$は、

${\frac {r(t)}{a}}=1-e\cos(\Omega t)+{\frac {3}{2}}e^{2}\sin ^{2}(\Omega t)+O(e^{3})$

である。これらは、離心率$e$が小さい場合、周転円の中心がケプラーの法則に従って、地球の周りを軌道長半径$a$, 離心率$e$の楕円軌道に沿って運動するとしたものに近く、$e$の一次のオーダーまで一致し、二次の項も極端に異なるわけではない。なお、仮に周転円の中心がケプラーの法則に従って回転した場合、

$\nu (t)=\Omega t+2e\sin(\Omega t)+{\frac {5}{4}}e^{2}\sin(2\Omega t)+O(e^{3})$

${\frac {r(t)}{a}}=1-e\cos(\Omega t)+e^{2}\sin ^{2}(\Omega t)+O(e^{3})$

である。この二つの式では、$e$は楕円の離心率である。エカントは、このように円運動一つで楕円運動を効率よく近似する。

プトレマイオスの理論と楕円軌道

もしもケプラーのエカントの理論をそのまま地球中心に書き直すと、周天円の中心は従円上から少しずれ、惑星の周天円上の回転の中心もまた別の点になる。しかしプトレマイオスの周天円は、既に述べたようにずっと単純である。そこで、地球と惑星の両方の軌道離心率は、重ね合わさって従円に反映されている。特に金星と火星では、両方の要素が同じ程度に影響している。

精度を最適にするには、従円の中心は地球と惑星の軌道離心率ベクトルの和だけ地球からずらし、エカントは外惑星の場合は惑星の、金星の場合は地球の軌道の焦点にとるのが良い。実際のプトレマイオスの理論では、離心円の中心が地球とエカントの丁度中間になるように取られていたので、上記の最適な配置にはならないが、実際の惑星と地球の距離の変動を良く近似している。

批判

クラウディオス・プトレマイオスの『アルマゲスト』『惑星仮説』では、円軌道は全て透明な硬い球体として物理的な実体を持ち、等速回転するとされた。もし周転円の中心が上で説明されたような運動をするのであれば、この従円に対応する球体は回転速度を時々刻々変えなければならず、この説明にそぐわない。その上、回転速度の変化を実現させる物理的な仕組みの説明も、特に示されていない。それどころか、宇宙論の書である『惑星仮説』では、エカントは言及されない。また、天界の自然な運動は地球を中心にする等速円運動しかないとするアリストテレスの自然学にも反する。この矛盾は、中世において度々取り上げられ、批判されてきた。

エカント批判には、そもそも周転円や離心円を認められないとするもの（エウドクソスの同心球説の改良を目指アルペトラギウスやイブン・ルシュドなど）と、等速円運動であれば地球を中心に持たないものでも可とする立場に分かれた。後者の立場のものとしては、ウルディーの補題による代替を考えたシリアの天文学者ムアイヤドゥッディーン・ウルディー、トゥースィーの対円による代替を考えたペルシアの碩学ナスィールッディーン・トゥースィー、両者を綜合してより複雑な水星の問題に取り組んだペルシアのシーラーズィー、これらを踏まえてより観測に合う月や太陽の距離の理論を作ったイブン・シャーティル、そしてニコラウス・コペルニクスがいた。

参考文献

• Neugebauer, O., A History of Ancient Mathematical Astronomy, Springer, 1975
• George Saliba (1996) Arabic planetary theories after the eleventh century AD :in Rashed, ed. (1996) Encyclopedia of the History of Arabic Science, vol.1. Routledge, pp. 59-128, arxiv.org
• Olaf Pedersen, A Survey of the Almagest, With Annotation and New Commentary ByAlexander Jones, Springer, 2011.

外部リンク

• Ptolemaic System at Rice University's Galileo Project
• Java simulation of the Ptolemaic System at Paul Stoddard's Animated Virtual Planetarium, Northern Illinois University