純正律
純正律(じゅんせいりつ、英語: Just intonation)は、周波数の比が整数比である純正音程のみを用いて規定される音律である。
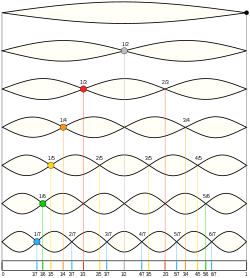
例えば純正律による長調の全音階は、純正完全5度 (3/2) と純正長3度 (5/4) を用いて各音が決定される。 すなわち、Cを基準とした場合、Cの3度上がE、5度上がG、次にGの3度上がB、5度上がD、さらにCの5度下がF、Fの3度上がAとなり、これらを1 オクターヴ内に配列することでハ長調の全音階が得られる。
上述の音階を以下に示す。大文字のTは大全音 (9/8)、小文字のtは小全音 (10/9)、sは半音 (16/15) の音程を表す。
| Note | Name | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 | |||||||||
| Cents | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 | |||||||||
| Step | Name | T | t | s | T | t | T | s | |||||||||
| Ratio | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 | ||||||||||
| Cents | 204 | 182 | 112 | 204 | 182 | 204 | 112 | ||||||||||
純正律の長所は、倍音のうなりを伴わない、単純な整数比による純正な和音が得られることである。 上記の例であれば、C-E-G、F-A-C、G-B-Dの三和音は4:5:6の比となり、三和音として最も単純な比を持つ。
短所は、音の組によっては、純正音程から著しく外れることである。上記の例ではD-Aの音程は純正完全5度 (3/2) よりも81/80(シントニックコンマ)狭い40/27となり、この音程を含む和音は非常に響きが悪くなる。そのため純正律では転調や移調が困難である。
もう一つの短所は、旋律の演奏に際しては、純正律では大全音 (9/8) と小全音 (10/9) の2種類の全音が存在するため、音階が不均等な印象を与え、また演奏が難しいことである。
これらの幹音から上に純正長3度の音程をとることで♯の派生音が、下に純正長3度の音程をとることで♭の派生音が得られる[1]。この結果、純正律においては全音階的半音(16/15、112セント)、半音階的小半音(25/24、71セント)、半音階的大半音(135/128、92セント)大リンマ(27/25、134セント)という4種類もの半音が存在する[1]。
純正完全5度 (3/2) と純正短3度 (6/5) を用いた純正律によるイ短調の全音階は以下のようになる。
| Note | Name | A | B | C | D | E | F | G | A | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 6/5 | 4/3 | 3/2 | 8/5 | 9/5 | 2/1 | |||||||||
| Cents | 0 | 204 | 316 | 498 | 702 | 814 | 1018 | 1200 | |||||||||
| Step | Name | T | s | t | T | s | T | t | |||||||||
| Ratio | 9/8 | 16/15 | 10/9 | 9/8 | 16/15 | 9/8 | 10/9 | ||||||||||
| Cents | 204 | 112 | 182 | 204 | 112 | 204 | 182 | ||||||||||
この場合、下属音のDはAの純正な完全5度下になるため、ハ長調のDより低くなる。つまり、純正律ハ長調の全音階においてそのまま主音をハ (C) からイ (A) に移しても、純正なイ短調の短音階にはならず、Dをシントニックコンマ低めなければならない[2][注釈 1]。一方で、純正律ハ長調の幹音(C,D,F,G)および派生音(E♭,A♭,B♭)から純正律のハ短調の音階を得ることができる[2][注釈 2]。このような面から、「平行調よりも同主調の方がより密接な関係にある」とする見解もある[2]。
純正律を可能とする楽器
編集日本の楽器メーカーであるヤマハでは、学校における合奏および合唱の指導において、特にロングトーン(持続音)のハーモニー[要曖昧さ回避]の改善を目的とした、ハーモニーディレクターおよびハーモニーキーボードという名称の電子キーボードを供給している。これらの製品では主キーの長調と短調を選択して、その三和音を平均律と純正律に近いチューニングに分けて、発音させることができるようになっている。またローランドでもシンセサイザーの一部製品(XPシリーズ、RSシリーズなど)において、平均律をセント単位で補正することで、純正律に近いチューニングを可能としている。
ヤマハ、ローランド、カシオの電子ピアノと電子オルガンの製品においては、平均律以外の各種古典調律とともに純正律の選択が装備されているものもある。
また、ヤマハが1951年から1982年まで販売していた第一世代ミュージックサイレンは、吹鳴のテンポが全体的に遅い事や、屋外への響きを重視していることから和音が得られやすい純正律を採用している。例えば、「家路」や「埴生の宿」、「花嫁人形」などその他吹鳴する際には制御装置や発音装置の構造で音が持続するように設計されている。
脚注
編集注釈
編集出典
編集- ^ a b 坂崎紀 (2017年9月18日). “純正律 「2.4. 全音が2種類!、半音が4種類!」”. early keyboard instruments. 音律入門. 2022年6月29日閲覧。
- ^ a b c 溝部國光『正しい音階 音楽音響学』日本楽譜出版社、1984年、39頁。ISBN 978-4-86060-901-6
参考文献
編集- 「純正律」『音楽大事典』 3 (シ~テ)、平凡社、1982年4月、1208-1211頁。国立国会図書館書誌ID:000001557638。